Ionization energy
The ionization energy of a chemical species, i.e. an atom or molecule, is the energy required to remove 1 mole of electrons from 1 mole of gaseous atoms or ions. Large atoms or molecules have a low ionization energy, while small molecules tend to have higher ionization energies.
The property is alternately still often called the ionization potential, measured in volts. In chemistry it is often referred to one mole of substance (molar ionization energy or enthalpy) and reported in kJ/mol. In atomic physics the ionization energy is typically measured in the unit electron volt (eV).
The ionization energy is different for electrons of different atomic or molecular orbitals. More generally, the nth ionization energy is the energy required to strip off the nth electron after the first 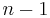 electrons have been removed. It is considered a measure of the tendency of an atom or ion to surrender an electron, or the strength of the electron binding; the greater the ionization energy, the more difficult it is to remove an electron. The ionization energy may be an indicator of the reactivity of an element. Elements with a low ionization energy tend to be reducing agents and form cations, which in turn combine with anions to form salts.
electrons have been removed. It is considered a measure of the tendency of an atom or ion to surrender an electron, or the strength of the electron binding; the greater the ionization energy, the more difficult it is to remove an electron. The ionization energy may be an indicator of the reactivity of an element. Elements with a low ionization energy tend to be reducing agents and form cations, which in turn combine with anions to form salts.
Electron binding energy (BE), more accurately, is the energy required to release an electron from its atomic or molecular orbital when adsorbed to a surface rather than a free atom. Binding energy values are normally reported as positive values with units of eV. The binding energies of 1s electrons are roughly proportional to (Z-1)² (Moseley's law).
Contents |
Values and trends
- Main article: Molar ionization energies of the elements
Generally the (n+1)th ionization energy is larger than the nth ionization energy. Always, the next ionization energy involves removing an electron from an orbital closer to the nucleus. Electrons in the closer orbitals experience greater forces of electrostatic attraction; thus, their removal requires increasingly more energy. Ionization energy becomes greater up and to the right of the periodic table.
Some values for elements of the third period are given in the following table:
| Element | First | Second | Third | Fourth | Fifth | Sixth | Seventh |
|---|---|---|---|---|---|---|---|
| Na | 496 | 4,560 | |||||
| Mg | 738 | 1,450 | 7,730 | ||||
| Al | 577 | 1,816 | 2,881 | 11,600 | |||
| Si | 786 | 1,577 | 3,228 | 4,354 | 16,100 | ||
| P | 1,060 | 1,890 | 2,905 | 4,950 | 6,270 | 21,200 | |
| S | 999.6 | 2,260 | 3,375 | 4,565 | 6,950 | 8,490 | 27,107 |
| Cl | 1,256 | 2,295 | 3,850 | 5,160 | 6,560 | 9,360 | 11,000 |
| Ar | 1,520 | 2,665 | 3,945 | 5,770 | 7,230 | 8,780 | 12,000 |
Large jumps in the successive molar ionization energies occur when passing noble gas configurations. For example, as can be seen in the table above, the first two molar ionization energies of magnesium (stripping the two 3s electrons from a magnesium atom) are much smaller than the third, which requires stripping off a 2p electron from the very stable neon configuration of Mg2+.
Ionization energy is also a periodic trend within the periodic table organization. Moving left to right within a period or upward within a group, the first ionization energy generally increases. As the atomic radius decreases, it becomes harder to remove an electron that is closer to a more positively charged nucleus. ionization enthalpy increases from left to right in a period and decreases from top to bottom in a group.
Electrostatic explanation
Atomic ionization energy can be predicted by an analysis using electrostatic potential and the Bohr model of the atom, as follows.
Consider an electron of charge -e and an atomic nucleus with charge +Ze, where Z is the number of protons in the nucleus. According to the Bohr model, if the electron were to approach and bind with the atom, it would come to rest at a certain radius a. The electrostatic potential V at distance a from the ionic nucleus, referenced to a point infinitely far away, is:
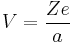
Since the electron is negatively charged, it is drawn inwards by this positive electrostatic potential. The energy required for the electron to "climb out" and leave the atom is:
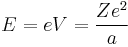
This analysis is incomplete, as it leaves the distance a as an unknown variable. It can be made more rigorous by assigning to each electron of every chemical element a characteristic distance, chosen so that this relation agrees with experimental data.
It is possible to expand this model considerably by taking a semi-classical approach, in which momentum is quantized. This approach works very well for the hydrogen atom, which only has one electron. The magnitude of the angular momentum for a circular orbit is:
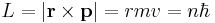
The total energy of the atom is the sum of the kinetic and potential energies, that is:
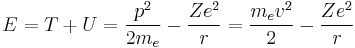
Velocity can be eliminated from the kinetic energy term by setting the Coulomb attraction equal to the centripetal force, giving:
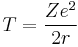
Solving the angular momentum for v and substituting this into the expression for kinetic energy, we have:
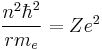
This establishes the dependence of the radius on n. That is:
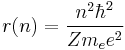
Now the energy can be found in terms of Z, e, and r. Using the new value for the kinetic energy in the total energy equation above, it is found that:
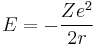
At its smallest value, n is equal to 1 and r is the Bohr radius a0. Now, the equation for the energy can be established in terms of the Bohr radius. Doing so gives the result:
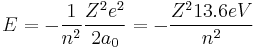
Quantum-mechanical explanation
According to the more complete theory of quantum mechanics, the location of an electron is best described as a probability distribution. The energy can be calculated by integrating over this cloud. The cloud's underlying mathematical representation is the wavefunction which is built from Slater determinants consisting of molecular spin orbitals. These are related by Pauli's exclusion principle to the antisymmetrized products of the atomic or molecular orbitals.
In general, calculating the nth ionization energy requires calculating the energies of 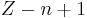 and
and 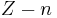 electron systems. Calculating these energies exactly is not possible except for the simplest systems (i.e. hydrogen), primarily because of difficulties in integrating the correlation terms. Therefore, approximation methods are routinely employed, with different methods varying in complexity (computational time) and in accuracy compared to empirical data. This has become a well-studied problem and is routinely done in computational chemistry. At the lowest level of approximation, the ionization energy is provided by Koopmans' theorem.
electron systems. Calculating these energies exactly is not possible except for the simplest systems (i.e. hydrogen), primarily because of difficulties in integrating the correlation terms. Therefore, approximation methods are routinely employed, with different methods varying in complexity (computational time) and in accuracy compared to empirical data. This has become a well-studied problem and is routinely done in computational chemistry. At the lowest level of approximation, the ionization energy is provided by Koopmans' theorem.
Vertical and adiabatic ionization energy in molecules
Ionization of molecules often leads to changes in molecular geometry, and two types of (first) ionization energy are defined – adiabatic and vertical.[1] The adiabatic ionization energy of a molecule is the difference between the energies of the neutral molecule and its positive ion, each in its vibrational ground state, and possibly with different equilibrium geometries.
The vertical ionization energy is the energy required to form a positive ion with the same geometry as the neutral molecule, corresponding to a vertical transition on a diagram of potential energy as a function of geometry. Such ionization is often accompanied by vibrational excitation. According to the Franck-Condon principle, vertical ionization is the most probable, since electrons move much more rapidly than nuclei and the ionized electron departs before the nuclei have time to adjust their position.
For a diatomic molecule the geometry is defined by one bond length. The removal of an electron from a bonding molecular orbital weakens the bond and increases the bond length. In Figure 1, the lower potential energy curve is for the neutral molecule as a function of bond length. The horizontal lines are vibrational levels with their associated vibrational wave functions. The upper curve is the ionized state, with its minimum energy further to the right since the bond length in the ion is greater. The adiabatic ionization is the diagonal transition to the vibrational ground state of the ion. Vertical ionization involves vibrational excitation of the ionic state and therefore requires greater energy.
See also
- Bragg-Gray Cavity Theory
- Electronegativity
- Ionization
- The work function is the energy required to strip an electron from a solid.
- Ion
- Koopmans' theorem
- Di-tungsten tetra(hpp) has the lowest recorded ionization energy for a stable chemical compound.
- Electron affinity
- Debye length